Difference between Deterministic and Stochastic Algorithms

The term algorithm is often used when IT people don’t want to explain how something works in detail. It’s commonly used as a wrapper for all the enigmatic things going on in software applications. First of all, this post will provide a preferably brief but exact definition of what an algorithm is. Second, I would like to explain the difference between a deterministic and stochastic (also known as probabilistic) algorithm design.

What is an Algorithm

The definition given by the Cambridge Dictionary defines an algorithm as follows:

a set of mathematical instructions or rules that, especially if given to a computer, will help to calculate an answer to a problem. To support your understanding of this algorithm definition, here an example:

Imagine you are playing a board game with some friends. Let’s assume that the rules stated in the manual are well known by everyone participating in the game. Theoretically, what every player does, once a move was performed, is verifying it intuitively. We do this by checking all the rules which this move was obeying to in this certain situation of the board game. For instance, was the player eligible to make the next move? Was the way the player performed the move legal? Is the board game in a legal state after the move was performed? In case any question cannot be answered with yes, you would interrupt the game and blame the player for cheating. Since this protocol will be conducted after every move in the exact same way, we can name it as an algorithm.

Another famous real-world example to illustrate an algorithm is a cooking recipe. It states all the activities to be executed in the applicable order which eventually will lead to the desired dish.

Deterministic Design

Algorithm design involves elaborating many different aspects like complexity, performance, or operating principles. The latter one can also be seen as design methodology, indicating how the algorithm aims to solve a given problem. A very simple version of this can be a deterministic design. It basically means that for the same input, the same output has to be generated. Let’s look at an example:

When we demand a calculator to compute the cross total of 123, it will output 6 as a result. The applied algorithm could involve the step-by-step summation of each digit from left to right. Now, this protocol acts always in the same way which is why we can be sure that the result will be 6 if we repeated the cross-total calculation of 123. We can do this infinite times and the result will always be 6 – that’s why we consider these algorithm families as foreseeable or deterministic.

Stochastic Design

Before we head to the behavior of stochastic algorithms, I should first explain briefly a certain class of problems. Presumably, you recognized that computers are pretty fast in calculating stuff in order to come up with the right solution. Sometimes, they just examine every possible answer in order to find the correct one (brute forcing). Funnily, there are still problems which have so many potential answers, that a supercomputer would have centuries to check all of them to return the best solution. In such cases, we talk about problems with a nondeterministic polynomial time hardness. In other words, there are no algorithms which could solve these kinds of problems in a polynomial time. To support your understanding, notice the picture below.

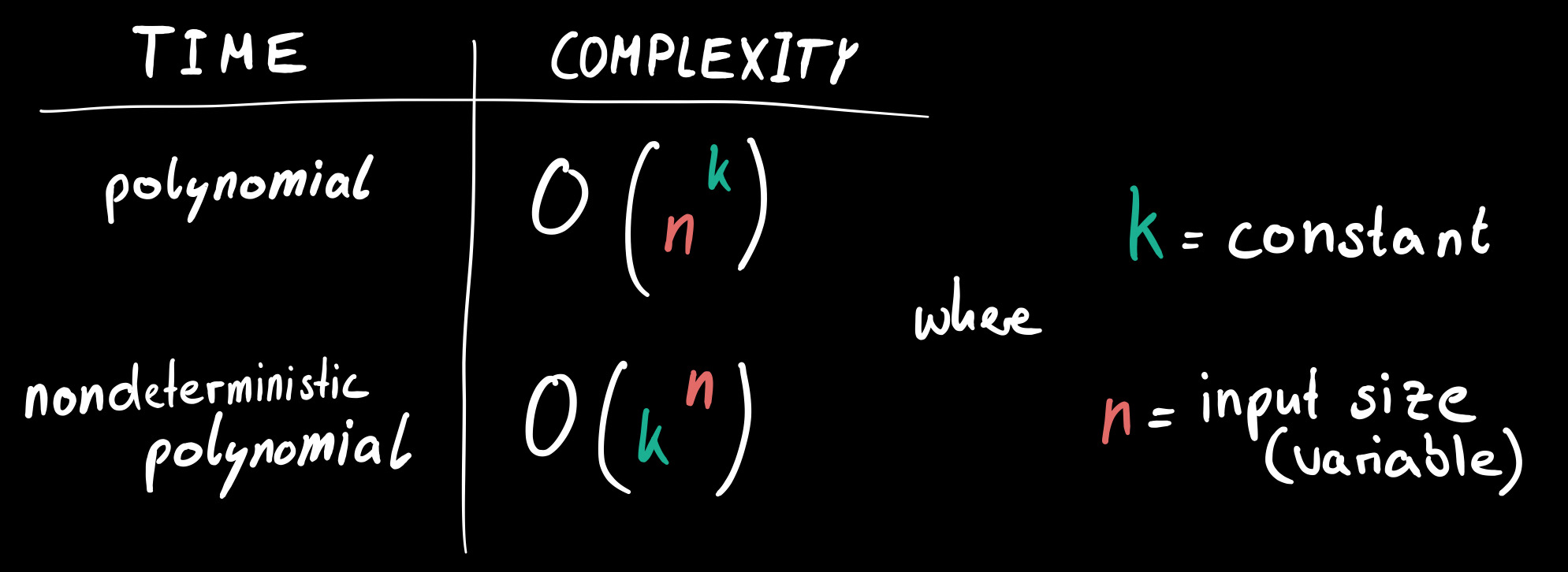
The classification, which problems can be solved in polynomial time and which cannot (nondeterministic polynomial time) is, by the way, a big issue for itself, named «p vs. np». In case you want to learn more about this problem, I recommend this article on Medium. One of the most famous ones is called the Travelling Salesman Problem (TSP). It’s about finding the shortest closed path (circuit) in a set of cities (vertices). Stochastic (or probabilistic) algorithms serve as a suitable tool to still come up with a decent solution. It probably won’t be the optimal one though. The key point in these kinds of algorithms lies in the incorporation of randomness during the computation process. The word stochastic originates from the Latin expression stokházomai which means something like «aim at a target» and «guess». So instead of a deterministic approach, where the algorithm’s steps remain the same, the stochastic approach always involves some unforeseeable decisions due to the influence of randomness. An iterative calculation process will return different outputs with the same input.

Deterministic vs. Stochastic

Algorithms can be seen as tools. Each tool has a certain level of usefulness to a distinct problem. In terms of cross totals, determinism is certainly a better choice than probabilism. When it comes to problems with a nondeterministic polynomial time hardness, one should rather rely on stochastic algorithms. Although, it probably won’t output the optimal solution, having at least one solution is still better than ending up with nothing.