Since I am one of the fellows 2023/24, I was recently featured in a portrait article on the WSS homepage. Among others, I talk about my research conducted during my Master’s thesis at IBM Research Zurich.
👀 See full article in English or German.

Since I am one of the fellows 2023/24, I was recently featured in a portrait article on the WSS homepage. Among others, I talk about my research conducted during my Master’s thesis at IBM Research Zurich.
👀 See full article in English or German.

The famous electronic peer-to-peer cash system called Bitcoin is an open-source protocol allowing individuals to store and transact units of the same named currency. Private and public key cryptography plays a central role in this value transfer system, which implies the importance of professionally managing the information about such keys.
This work elaborates on the essential prerequisites to understand this relatively new technology that combines elements from the fields of computer science, cryptography, mathematics, and game theory. In doing so, crucial general and Bitcoin-specific terms are defined and contextually explained.
The central part of this work addresses the outline of different Bitcoin interaction means, commonly known as wallets. The structure of the presented wallet types orients itself alongside a potential user’s experience. Besides defining explanations and examples of use cases, this work outlines advantages and disadvantages concerning security and privacy.
The start concerns two wallets that target beginners in the field of Bitcoin. The concept of online accounts is elaborated and attention is drawn to the inherent need to trust when using them. Also, the relatively primitive type of paper wallets is surveyed.
For a more intermediate interaction with this peer-to-peer cash system, the concept of software wallets, in general, is explained and examples are provided. The bridge from single-address paper wallets will be drawn to the more sophisticated multi-address wallets enabled through rooted key derivation techniques. Designated computer devices that solely serve the purpose of managing keying material, known as hardware wallets, represent another intermediate wallet type discussed in this work.
Last, advanced topics are discussed that further leverage the security and privacy of someone’s interaction with Bitcoin. One concerns the setup of a self-managed Bitcoin full node. This undertaking not only harmonies with the concept of verification over trust but also allows for the complete exclusion of any third party between wallet communication. Equally advanced is the concept of multi-signature wallets, which is discussed at the end of this work.
Keywords: Bitcoin · Software Wallets · Hardware Wallets · Private Key Management
In October 2008 a user with the pseudonym Satoshi Nakomoto introduced in an email to The Cryptography Mailing List the idea of a peer-to-peer electronic cash system that no longer requires trusted parties and simply works based on software and mathematical rules
At the beginning of 2009, Nakamoto published a post in the P2P foundation forum to invite the public to explore and download the first software version of Bitcoin

Looking back at this early stage in the course of Bitcoin’s evolution, these posts represent contemporary history
Nakamoto’s peer-to-peer electronic coin that can be used to transfer units from one place to another without relying on a necessarily trusted party in between succeeded. Numerous individuals and even institutions benefit from it by using it as a store of value, medium of exchange, or even unit of account. These purposes are commonly known as the three purposes of money.
An idea, textual explanation, software source code, mathematical laws, and intrinsic interest of individuals form the basis of this success. One concludes that everything that defines Bitcoin is simply information. Apparently, Nakamoto intended to free this information to the world and therewith pass the point of no return. Everyone and everything that can process this information will be able to interact with Bitcoin. No permission has to be obtained, nobody and nothing needs to be trusted, nor could by any authority.
It must have been Nakamoto’s desire to enable such a complete self-determined interaction for absolutely everyone without any prevailing party involved. This may be why the pseudonymized authorship has not been revealed until today and possibly never will. A potential association of Bitcoin with any form of existing individual or collective would automatically increase their influential power, regardless of whether indented. Additionally, this would also represent a target for powerful institutions and governments that may repudiate the idea of an uncontrollable, transparent, and censorship-free value transfer system. Ultimately, it is of no meaning who published this idea. What is essential, however, is that millions of people absorbed it and continue to use it because they intrinsically want to use it.
This work should lower the admittedly high barrier to entry to Bitcoin, again increasing its accessibility. This is done by covering different ways to interact with this peer-to-peer system with different security and privacy levels. While aiming for practicality, a generic storyline will be narrated where the readership identifies itself. The story told reflects the questions and challenges a new Bitcoin user will sooner or later be faced with. This undertaking structures in three stages, namely beginner, intermediate, and advanced. Eventually, the readership has gained the necessary information to confidentially start interacting with Bitcoin using the approaches that best fit the user’s needs.
The present work does not address money’s historical, social, and economic aspects and its relation with Bitcoin. Interested readers in these topics can refer to Von Mises
This thesis studies three different approaches to cluster time series data using the unsupervised pattern recognition method called hierarchical clustering. The underlying data constitute long-term water temperature measurements of several Swiss water bodies and originates from metering stations which are managed by the Federal Office for the Environment in Switzerland.
The goal is to group these stations according to the resemblance of their hydrologic temperature curve over a period of ten years with a ten-minute sampling rate of detail. Stations that exhibit very similar short-term as well as long-term temperature behaviour and evolution over time should be grouped into the same clusters. These clusterings should provide a better understanding of the data heterogeneity received from the various metering stations in Switzerland and support future decisions regarding the integration of new stations.
The first part of this work addresses the characteristics of time series data and surveys the field of pattern discovery techniques. The procedure of hierarchical clustering is explained in detail as it is the chosen technique applied for the cluster analysis of this thesis. Furthermore, four internal cluster validity indexes used to assess the quality of a cluster composition are elaborated.
The main part addresses the applied distance measuring strategies and assesses the quality of the received clustering results. Defining the level of similarity between two data objects is a fundamental concept in pattern recognition disciplines. This thesis elaborates the two shape-based strategies Pairwise Distance and Dynamic Time Warping and the feature-based strategy Discrete Wavelet Transformation. The cluster analyses are generated with different data aggregation levels and linkage methods. Finally, the various clustering approaches are challenged based on a forecast deviation analysis. This facilitates conclusions about the quality of the various cluster compositions in the form of quantifiable measures.
Keywords: Hydrology · Water Temperatures · Hierarchical Clustering · Time Series
This paper surveys the different approaches in pattern recognition (PR). After the fundamental idea of PR is stated, a taxonomy landscape is presented which divides into three families, namely statistical, structural, and hybrids. The first represents a well-researched topic in PR which engendered popular and efficient supervised and unsupervised pattern discovery algorithms. The second family addresses techniques to find patterns in structurally represented data using graphs that allow capturing the information of relationships among objects. Thirdly, the hybridization of the prior two families will be discussed. This includes the elaboration of transformation methods that allow to embed a graph into a vector space using graph kernels or graph embedding.
Keywords: Statistical Pattern Recognition · Structural Pattern Recognition · Graph Kernels · Graph Embedding
PR methods aim to find patterns in data which are hard or even infeasible to discover for humans. Although there are many different approaches to accomplish this, it always requires the derivation of a similarity or dissimilarity indicator among the data objects. Based on this measurement, arrangements can be built that group similar data objects together and distance dissimilar data objects from themselves. In classification disciplines, these groups are commonly referred to as classes, in clustering disciplines clusters.
The science of recognizing patterns in data started to emerge in the late sixties. A popular paper by Fu (1980)
A crucial part of PR is the representation of the underlying information in order to be processed by a computational algorithm. In general, one distinguishes between statistical and structural data. Either case has advantages and disadvantages regarding the task of emerging patterns in this data. Furthermore, the applicable algorithmic tool repository differs as well. This survey constitutes popular PR methods in both data representations and reviews ideas to link them together.
First of all it has to be said that performance in SQL queries is depending on many different aspects such as the underlying database management system (DBMS), the database’s architecture or the IT infrastructre you are working in.
Firt of all I would like to point out that the rules and optimizations measures presented are either based on experience in my professional environment or backed up by indicated literature. Furthermore, it has to be said that other DBMS might work with other data handling principles and methods. Hence, the guidelines below may do not have any influence or even lead to less performing queries. The system environment, as well as the hardware, must also be regarded as influencing factors which may temper the effect of the advice below.
Personally, I made great experiences applying these rules and optimization techniques which is why I would like to share it.
Shortly after some first tries with SQL one will realize that there exist many different ways to reach the desirable result. However, one should still be aware of some basic rules when high performance is required. Having said that the rules explained in this section cannot be regarded as a silver bullet for all queries, but one will generally not be worse off applying them.
Imagine a database containing two tables, one called tbl_People including names, gender and addresses of all people from the world and the other one, which is related [1:n] called tbl_Disease including all possible diseases existing. The aim now would be to show all men which live in the United States and are diagnosed with lung cancer, which in this case would be a very rare disease. Now, when constructing the query, an optimized way would be to firstly filter by the smallest multitude, in this case undoubtedly the illness, before joining the entities. This leads to a substantial reduction of records in the very first pass through. Secondly, it would be recommendable to further minimize the list so that only masculine individuals are left. Finally, one could filter for the country. The statement \eqref{eq:f1} expresses this using relational algebra notation.
In contrast to the statement \eqref{eq:f1}, notice the suboptimal version \eqref{eq:f2} below, where the two entities are joint at first and then filtered in a not ideal order:
It is all too easy to code a query with SELECT*, which then will project all columns available, regardless if they are needed or not. But as is often the case in programming, operating in an optimal way means working with only the minimum of recourses need for a certain task. Imagine a table with 150 columns which all get invoked in a query despite only three columns are actually needed. This requires far more processing power which simultaneously takes CPU power away from other tasks. Hence, only put columns in SQL statements which either are necessary for further calculation or shall be outputted for informational reasons. This will keep data processing light and affects the performance of the query in a positive way
Adhoc is Latin and means for this purpose. Especially in MS Access, for instance, it is sometimes easier to write the SQL statement directly in the executed code than to create a predefined query and invoke it as a database access object (DAO). The reason why this is not advisable is because of the so-called execution plan which the DB will devise for each query after the first execution. Simplified expressed, it is a set of instructions which indicate how to best execute the query
Besides rules about how to construct a query the most efficient way, performance is often also a question of the database’s architecture. Since renovation a DB is a arduous undertaking, I would like to introduce four techniques to increase query performance that do not require dangerous architectural database manipulations.
The desirable result of data selection often cannot be made within one single query. When being faced with sophisticated queries which additionally shall be displayed in the system and react to the user’s input immediately and in real time, the usage of temporary tables is highly advisable. It may be a little bit costlier to develop but it can yield impressive gains
Instead of processing an intricate SQL statement which may involve many different tables with a big relation chain over and over again, the results can initially be written in a temporary table which then will be shown to the user. After he concluded all modifications, the data can be compared and eventually written back in the appropriate tables. Besides better performance, this approach provides the advantage of being able to draw on a temporary data state when it comes to debugging.
Another use case which will be suited to temporary tables occurs when a table should be joined to a larger table, where a condition must be considered, one can gain a performance improvement by pulling out the subset of data needed from the large table into a temp table and joining with that instead
A guiding principle regarding the application of temporary tables is the characteristic that no productive data should be affected while operating with this method. Consequently, the content of these type of tables should always be considered as erasable at any time due to its intermediate purpose.
Imagine a movie collector is looking for a specific film in his personal collection. Unfortunately, he did not sort the items regarding any order which forces him to look through all DVDs he owns. This issue would not have occurred when he initially would have sorted his collection alphabetically or, even better, numbered each item and list it together with its storage location on in a book. Although this would obviously cost effort to create such a register as well as maintaining it, such a tool would surely make searching for a DVD a lot easier and faster. This analogy explains quite well the principle of indexes on tables. Applying them on important columns in a table, a so-called shadow table will be initialized in the background which then helps the database to find specific records much faster. To support the understanding of this tool better, please note the following illustration
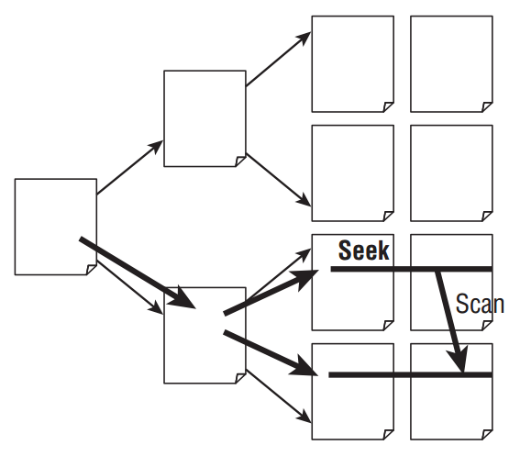
Instead of going through all the rows in a table to find a specific record, the database is able to cut the amount of data piecemeal down. Eventually, only a small extent of all tuples must be browsed to return the searched value. In general, it is recommendable to always initiate indexes on columns which often get sorted or filtered by, especially when the column contains text instead of numbers. Furthermore, they should also be deployed on columns which are responsible for establishing the relationship between entities, in particular, Foreign Keys.
Data should always be stored fully normalized when constructing a database. In this section, however, I will outpoint an exception when it is more useful to actively elude the principle of storing each information only once. Doing this, we operate with so-called redundant data.
It sometimes can be very helpful to store a Primary Key in form of a copy in a table which is linked to the original table through a long relation chain as it can occur in deep hierarchies, for instance, illustrated in the figure below.
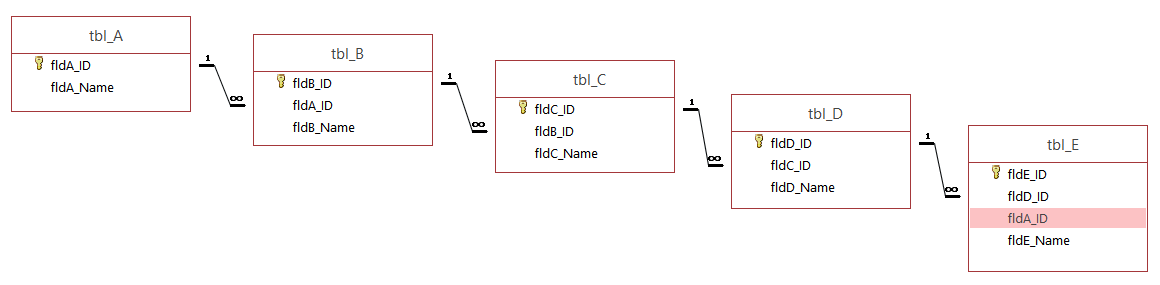
When the appropriate A-name of an E-object shall be queried, the database has to go through the entire relation chain to return the correct value. But listing the A-ID in tbl_E as a copy, provides the possibility to shorten this query procedure significantly as indicated below.
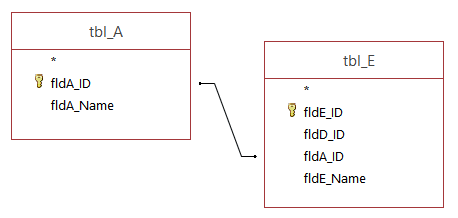
Nonetheless, it has to be said that this approach is not recommendable in data hierarchies with high alternation rate since each change has to be updated manually in the copy-field. However, in other Database Management Systems like MS SQL Server, such update transactions can be done automatically by so-called triggers
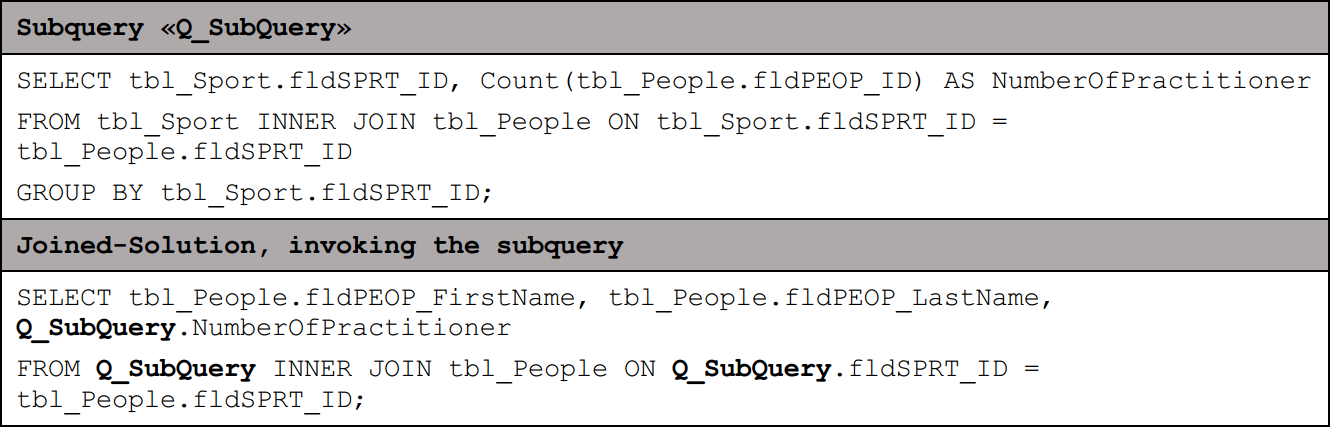
When a high data cascading is present, it often leads to a higher executing performance when the query is engineered with subqueries, in other words, predefined queries which then get joined to the next query. Another possibility would be to insert one SQL statement directly in the next SQL statement and save this as one query. In doing so, one has constructed a so-called nested select, which can decrease the performance of the data processing. Hence, it is generally the better approach to define only one statement per query and save them individually. Depending on the database technology you use, it would then even be possible to exactly allocate each single subquery to different server’s processors. This allows a non-sequential execution of the subqueries which means the whole process gets completed after the slowest query succeeded
For instance, if the aim would be to return a list with all people’s first and family names including the number of other persons who are practicing the same sport as themselves. As this evaluation requires a subquery which will depict the appropriate number of participators each sport, two approaches arise regarding solve this issue.
When applying the nested select approach, the SQL statement would look like the following:
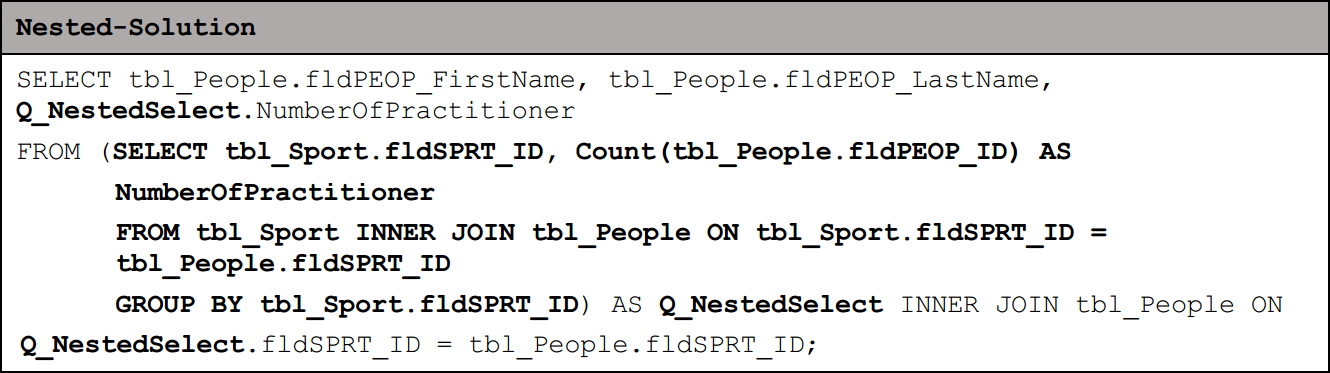
The bold section highlights the subquery which is in this case constructed in a nested way.
To visualize the more efficient way of solving the task, please consider the alternative solution below, in which the subquery gets invoked by a second query:
At a first glance, query performance might not seem a necessary issue to cope with but once a certain data volume is transcended, this topic will become more and more important. This article provides a small repertoire of possible optimization solutions which eventually can be adopted to its individual use case. Nonetheless, it has to be said that I only touched the surface of database science. Considering all the numerous different database management systems somehow operate differently than others, it would hardly be possible to write down a master solution for high performing SQL queries. Anyways, you now know about some basic tools to tune your SQL statments in order to decrease waiting times.
]]>The definition given by the Cambridge Dictionary defines an algorithm as follows:
a set of mathematical instructions or rules that, especially if given to a computer, will help to calculate an answer to a problem. To support your understanding of this algorithm definition, here an example:
Imagine you are playing a board game with some friends. Let’s assume that the rules stated in the manual are well known by everyone participating in the game. Theoretically, what every player does, once a move was performed, is verifying it intuitively. We do this by checking all the rules which this move was obeying to in this certain situation of the board game. For instance, was the player eligible to make the next move? Was the way the player performed the move legal? Is the board game in a legal state after the move was performed? In case any question cannot be answered with yes, you would interrupt the game and blame the player for cheating. Since this protocol will be conducted after every move in the exact same way, we can name it as an algorithm.
Another famous real-world example to illustrate an algorithm is a cooking recipe. It states all the activities to be executed in the applicable order which eventually will lead to the desired dish.
Algorithm design involves elaborating many different aspects like complexity, performance, or operating principles. The latter one can also be seen as design methodology, indicating how the algorithm aims to solve a given problem. A very simple version of this can be a deterministic design. It basically means that for the same input, the same output has to be generated. Let’s look at an example:
When we demand a calculator to compute the cross total of 123, it will output 6 as a result. The applied algorithm could involve the step-by-step summation of each digit from left to right. Now, this protocol acts always in the same way which is why we can be sure that the result will be 6 if we repeated the cross-total calculation of 123. We can do this infinite times and the result will always be 6 – that’s why we consider these algorithm families as foreseeable or deterministic.
Before we head to the behavior of stochastic algorithms, I should first explain briefly a certain class of problems. Presumably, you recognized that computers are pretty fast in calculating stuff in order to come up with the right solution. Sometimes, they just examine every possible answer in order to find the correct one (brute forcing). Funnily, there are still problems which have so many potential answers, that a supercomputer would have centuries to check all of them to return the best solution. In such cases, we talk about problems with a nondeterministic polynomial time hardness. In other words, there are no algorithms which could solve these kinds of problems in a polynomial time. To support your understanding, notice the picture below.
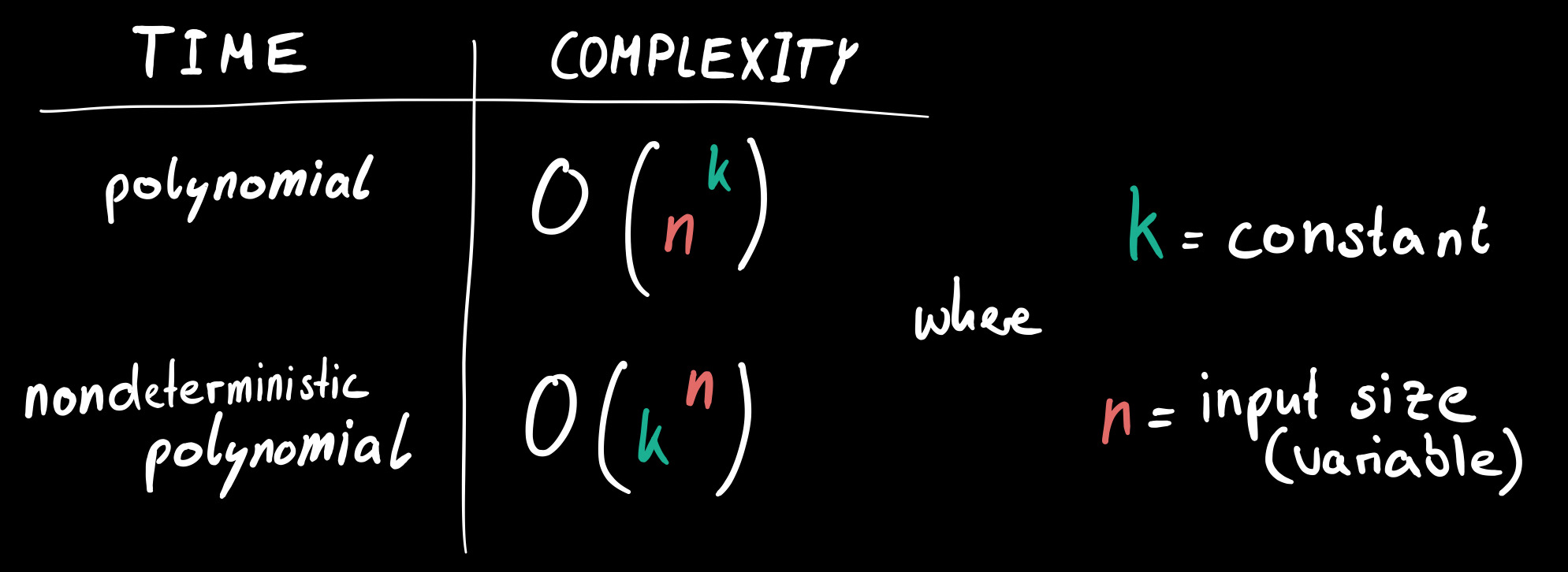
The classification, which problems can be solved in polynomial time and which cannot (nondeterministic polynomial time) is, by the way, a big issue for itself, named «p vs. np». In case you want to learn more about this problem, I recommend this article on Medium. One of the most famous ones is called the Travelling Salesman Problem (TSP). It’s about finding the shortest closed path (circuit) in a set of cities (vertices). Stochastic (or probabilistic) algorithms serve as a suitable tool to still come up with a decent solution. It probably won’t be the optimal one though. The key point in these kinds of algorithms lies in the incorporation of randomness during the computation process. The word stochastic originates from the Latin expression stokházomai which means something like «aim at a target» and «guess». So instead of a deterministic approach, where the algorithm’s steps remain the same, the stochastic approach always involves some unforeseeable decisions due to the influence of randomness. An iterative calculation process will return different outputs with the same input.
Algorithms can be seen as tools. Each tool has a certain level of usefulness to a distinct problem. In terms of cross totals, determinism is certainly a better choice than probabilism. When it comes to problems with a nondeterministic polynomial time hardness, one should rather rely on stochastic algorithms. Although, it probably won’t output the optimal solution, having at least one solution is still better than ending up with nothing.
]]>Before digging into the code, let’s briefly explain this appalling problem.
Imagine you defined some locations on a map. Now, you want to travel through all of them within one journey while trying to keep the overall distance at a minimum. Which order would you choose? This may sound like an easy question at first glance. It actually is when talking about three, five or six cities. But what if we talk about 50, 100 or even 10’000 cities? Then you realize how hard this problem is.
You might think, we have computers, so let’s let them do the work. Unfortunately, it’s not that easy because the TSP belongs to a special kind of problem having a so-called non-deterministic polynomial-time hardness.
Here is why:
Cities n | Possible Solutions (n−1)!/2 |
|---|---|
| 5 | 12 |
| 8 | 2'520 |
| 15 | 43'589'145'600 |
| 50 | 304'140'932'017'133'780'436'126'081'660'647'688'443'776'415'689'605'120'000'000'000 |
As you can see, the number of possible solutions increases quickly in unimaginable spheres. These are such high numbers that computers would need multiple decades to check all variations just for determining the optimal solution.
In contrast to conventional problems, the best solution is not known in advance. Think of a Sudoku: it may demand a lot of intellectual power and time, but once completed, you are easily able to check if the (only) solution is given. That’s not the case in the TSP. You will find a more comprehensive explanation of such NP-problems on Wolfram. Additionally, I recommend this video – it may lower the level of weirdness for you (or increase it…).
Solving extraordinary problems demands extraordinary approaches. One is a so-called genetic algorithm (GA). Its logic is based on the natural selection seen in evolution. A key aspect is «the survival of the fittest», as Darwin once stated. Before looking at an implementing of a GA, I kindly invite you to read a bit of theory regarding the algorithm’s structure and behavior.
An element is an exact definition of how to solve the problem. Referring to the TSP, this would be a specific path or route, going through all the cities. This is a possible solution, but it is not necessarily the best one.
A gene represents the smallest entity in the whole GA. Knowing that an element defines a concrete solution, a gene is one single component of it. Adapted to the TSP, one city or stop within an element is considered to be a gene.
A set of elements forms a population. The number of elements instantiated defines the population’s size. When creating a new population, all elements should be constructed completely at random. Subsequently, the GA tries to evolve its population further in order to develop better elements.
A current state of a population can be seen as a generation. When evolving the population further, we generate new generations. In other words, a generation is a specific set of elements held in the population.
According to Darwin, only the fittest will survive. To evaluate which elements are more likely to survive, we have to assess the quality of each element’s solution in relation to all other solutions. In doing this, we are able to indicate which solutions are better and which are worse, and we can award each of them with an appropriate fitness value. In TSP, the paths with the smallest total distance must be rewarded with the highest fitness. In other problems, this fitness function may differ.
Since we try to stimulate our population to evolve a more sophisticated and better version of itself, we should wisely select the elements which may survive a generation. Obviously, we want the genes of those elements with a higher fitness to survive while those with a poor fitness to cease.
With just determining the fitness and selecting the fitter elements, we did not optimize our solution to the TSP yet. Therefore, we will apply crossover, like its done in nature during the mating season. This enables to bequeath the qualitative good genomes of two pretty fit elements (depends on the selection) to a new one, which eventually will be part of the population’s next generation.
As an element refers to a specific path in TSP, we extract a random sequence of a fit element’s path (parent I) and put it into a new element (child). Then, we fill the remaining slots with path fragments (genes) of another fit element (parent 2). Doing this, we hopefully increase the possibility of having a child who is fitter than his parents.
Like in the real world, the evolution is influenced by some mutated genomes. By pairing parent AAAA with parent BBBB, we will end up with any kind of A-B-combination, but we will never get a C part in it. Hence, it is advisable to enforce some mutation in a GA.
Once we bred our child element in the TSP, we simply switch the order of the vertices (the genes), representing a concrete path, only very little but randomly.
The last and most important part of a GA is the act of repetitively creating new generations (evolving the population), as this is the only way to boost evolution in an advantageous direction. In doing this, we hopefully will replace the randomly constructed elements in our initial population with fitter ones over time. However, there is a good chance that our initial population will get stuck in an insufficient level of quality. In such a case, we only can hope for a lucky mutation to receive a significant fitter child element, but then we solely rely on randomness, which is not a good approach in such an enormous problem. To tune our GA, it is good practice to discontinue the evolution process of a population after a certain amount of generated generations, for instance, 100 in number, and start with a completely new population. Since the new population has to initiate its elements, we re-introduce a great amount of randomness, which hopefully yields a better solution when evolving this population again 100 times.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//take a guess
bestPath = randomPath;
while(!stop) {
//create a new population
Population pop = new Population;
//evolve population a limited number of times
for (int i=0 ; i < 100 ; i++){
//create the next generation
pop.evolve;
//retrieve the generation's best solution
Path p = pop.getFittestPath;
//compare it with the overall best solution
if(p.distance < bestPath.distance){
//we've found a better solution
bestPath = p;
GUI.repaint(bestPath);
}
}
/*Despite we may have developed an outstanding population,
*we stop evolving it here and start from scratch again.
*Possible stopping criterias could be a certain amount
*of newly generated populations or a reached threshold in
_the distance optimization of the new best path. _/
}
Since a GA is a heuristic approach to solve NP problems, the solution’s quality, as well as the time frame needed to reach a good solution, strongly depends on the custom configuration of some constants (parameters).
For instance, choosing a high population size increased the possibility of finding a fitter element but it also raised the computational work. In a TSP with 5 vertices, a population size of 200 would be nonsensical as there are only 5! = 120 possible solutions.
Another important constant is the mutation rate. The level of randomness influencing the GA’s effectiveness is directly linked to it. The more mutation we put in, the fewer genomes will survive a generation identically. It is advisable to keep the rate low since crossing over fit parents to birth an even fitter child would become superfluous and the whole process would resemble more of an inefficient brute force attempt.
To avoid the problem of getting stuck with an unfavorable population, the evolving process should be limited to a maximum number of generations. Once reached, the GA simply initializes a complete new population. In doing this, all elements are defined with a big amount of randomness. Therewith, we do not gamble away the chance of discovering entirely different solutions. Based on experience, a value between 50 and 200 is a good limitation for the number generations evolved.
In this chapter, I would like to explain some significant code extracts of my TSP implementation. In order to be more specific, I name from now on a population’s element as a path. Such a path object in my solution only holds integer values in an array, which corresponds to an index in the set of vertices (which is an ArrayList). Additionally, I aimed to calculate an optimal Hamiltonian path instead of the conventional closed path (circuit) in TSP. Please be aware, there are numerous other ways to implement these extracts in Java, but here comes mine.
When initiating a population, I would like to randomize the content of all paths in my population.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
private void shuffle(int nlntensity) {
int nMax = this.getLenghtQ;
int nlndexA = -1; //arbitrary
int nlndexB = -1; //arbitrary
boolean lExit = false;
if(nMax == 1) {
//no need to swap
lExit = true;
}
if(nMax == 2) {
//swap once
this.swap(0, 1);
lExit = true;
}
if (! lExit) {
//swap two elements randomly a certain number of times
for( int i = 0 ; i <= nlntensity ; i++ ) {
//set indices equal
nlndexA = nlndexB;
//find two different indices
while(nIndexA == nlndexB) {
//choose two indices randomly
nlndexA = (int)(Math.floor(nMax _ Math.random()));
nlndexB = (int)(Math.floor(nMax _ Math.random()));
}
//swap those two
this.swap(nIndexA, nlndexB);
}
}
}
Ultimately, making two vertices changing its place can simply be achieved by swapping them.
1
2
3
4
5
private void swap(int a, int b) {
int temp = this.Order[a];
this.Order[a] = this.Order[b];
this.Order[b] = temp;
}
I also make use of the shuffling function when it comes to mutation. In this case, the intensity of mingling is linked to the mutation rate which is a constant provided by the user.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void mutate(double nMutationRate) {
int nlntensity = 0;
//when mutation rate is 0.4, only 40% of the path be changed
int len = this.getLengthQ;
double a = Math.floor(len \* Math.abs(nMutationRate));
nlntensity = (int)(a);
/_since the mutation will simply be executed by swapping
elements, we have to divide the intensity by
two (one swap = two changes) _/
nIntensity = nIntensity / 2
this.shuffle(nlntensity);
}
Probably the most important part in the GA is the selection procedure. In order to make the next generation of a population more sophisticated, we have to pick paths wisely before crossing them. One implementation to do the selection could be the following.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//the aim is, to pick a path with a better fitness
//more likely than a path with a smaller fitness
private static Path pickOne(Arrayl_ist<Path> list) {
Path aReturn = null;
int index = 0; //assumption
double r = Math.random();
/\*\*
_ imagine we would have two elements in the list.
_ The first element has a fitness of 0.9, the
_ second one of 0.1. Consider the fact, that the
_ fitness indicates (rather obvious) how well an
_ element fits. Hence we misuse this value as the
_ probability of being picked. The random method
_ returns a value between 0.0 and 1.0, which gets
_ stored in the variable 'r'. Now, the probability
_ that we will oversee the first well fitting
_ element (e.g.: fitness of 0.9) resides by 10%,
_ since in this case 'r' must be between 0.91 and 1.0.
_/
while (r > 0) {
r = r - list.get(index).getFitness();
index++;
}
//take previous one (the one which caused the loop exit)
index--;
//get the path
aReturn = list.get(index);
return aReturn;
}
When dealing with a large population size, I advise against using this method. Since the sum of all fitness values in the population equals 1.0 (proportional allotment), every single value would be extremely small. Consequently, the break-out of the while-loop will rather be based on arbitrariness than on a wise selection. Therefore, I implemented another method, which is admittedly less spectacular than the first one, but I experienced it as more expedient.
1
2
3
4
5
6
7
8
9
10
11
12
private static Path pickRank(ArrayList<Path> list, int nlndex) {
Path aReturn =null;
ArrayList<Path> clonedList = new ArrayList<Path>(list);
/_sort paths according to their fitness
in descending order (using lambda) _/
clonedList.sort( (pi, p2) -> Double.compare(p2.getFitness(), pl.getFitness()) );
//get the required path
aReturn = clonedList.get(nlndex);
return aReturn;
}
After the provided list of paths was sorted by its fitness in ascending order, this static function is able to pick a path by its rank. In first place is the fittest path, in second place the second-fittest path and so on. Therewith, I have the opportunity to pick the two fittest paths in the population and create all the child paths for the next generation based on them.
Once two paths have been picked, I cross them over. The number of genes originating from the first path, respectively from the second path, is defined randomly. Alternatively, one could also set the shares to 50%.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
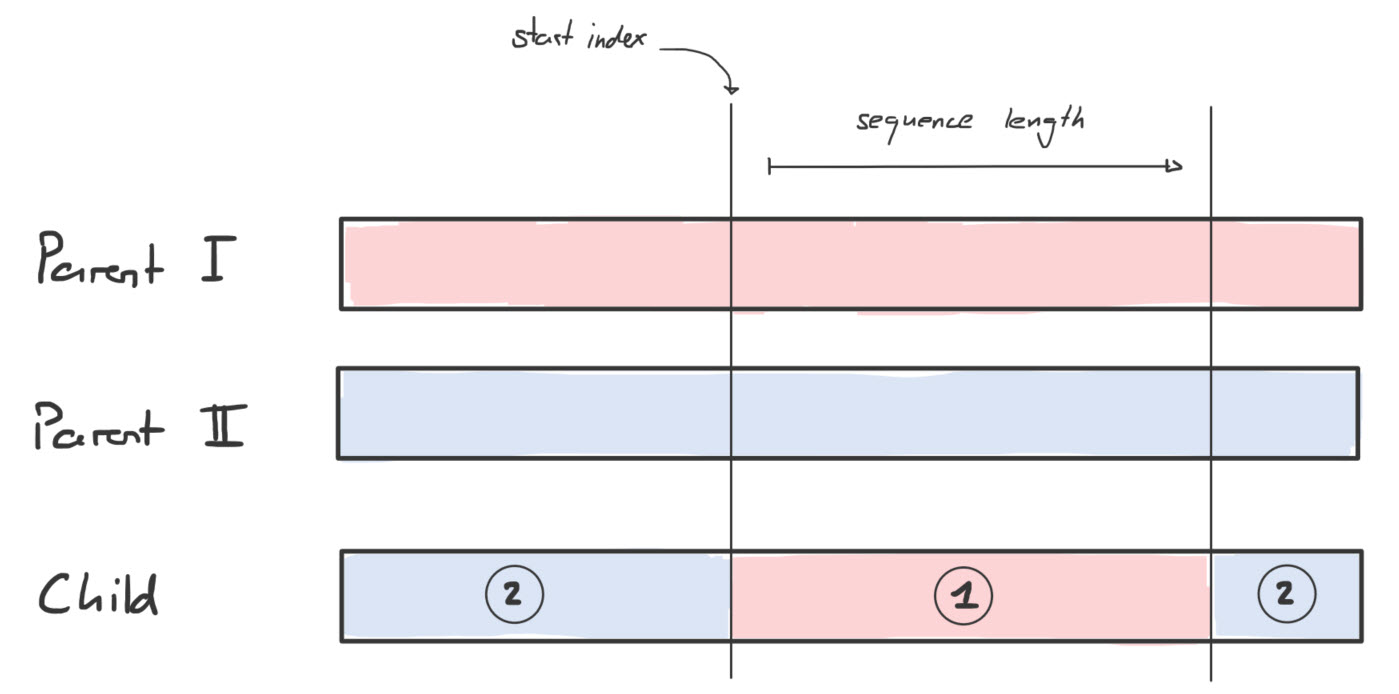
private static Path cross(Path pi, Path p2) {
Path aReturn = null;
int nLength = pl.getLengthQ;
int nSequenceLenght = (int) (nLength \* Math.random());
//set minimum length
if(nSequenceLenght == 0) {
nSequenceLenght = 2;
}
//decrease length
if(nSequenceLenght == nLength) {
nSequenceLenght -= 2;
}
//define start index randomly
int nStartlndex = (int) ((nLength-nSequenceLenght) \* Math.random());
//initiate a new order (child path)
int[] order = new int[nLength];
//put -1 into each slot as a placeholder
for (int i=0 ; i < Length ; i++) {
order[i] = -1;
}
//fill in genome of first parent path
for(int i=nStartIndex ; nSequenceLenght > 0 ; i++) {
order[i] = pl.get(i);
nSequenceLenght--;
}
//fill in genome of second parent path
int n=0;
for (int i=0 ; i < Length ; i++) {
if (order[i] == -1) {
//fillable slot found
boolean lExit=false;
while(!lExit) {
//check if vertex-index already included
if (Path.contains(order, p2.get(n))) {
n++;
} else {
lExit = true;
}
}
order[i] = p2.get(n);
}
}
aReturn = new Path(orden);
return aReturn;
}
Since both the start index and the sequence length are arbitrarily defined, my child path could be composited in various ways. The picture below visualizes one of them.
After exploring the components of a GA, the cooperation of them, using the PickOne method, would look like this.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void evolve() {
AmayList<Path> ps_new = new ArrayList<Path>();
this.assessFitnessQ;
for (int i=0 ; i < this.ps.size() ; i++ ); {
Path pi = pickOne(this.ps);
Path p2 = pickOne(this.ps);
Path p3 = cross(plj p2);
p3.mutate(this.nMutationRate);
ps_new.add(p3);
}
this.ps = ps_new;
}
To make usage of the more target-aimed method PickRank, I created the following alternative.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void evolve2() {
ArrayList<Path> ps_new = new ArrayList<Path>();
this.assessFitnessQ;
Path pi = pickRank(this.ps, 0);
Path p2 = pickRank(this.ps, 1);
while(ps_new.size() < this.ps.size()) {
Path p3 = cross(plj p2);
p3.mutate(this.nMutationRate);
ps_new.add(p3);
}
this.ps = ps_new;
}
The genetic algorithm approach is just one way to tame the travelling salesman problem. From my point of view, its parallels to the evolutionary process in the real world make it comprehensible and fun to implement. For sure, there are other interesting problem-solving approaches like the so-called simulated annealing or ant colony optimization algorithms.
In case you would like to dig deeper in this fascinating TSP, I recommend exploring this page. It provides historical information, other solving concepts, solution quality assessments and more.
PEstimator is an Java application which approximates the irrational mathematical constant Pi. The base for the approximation is a quarter circle within a rectangle. On this painting, points will be added iteratively. The ration of the number of points within the quarter circle to the total number of points, multiplied by four equals Pi over time, as shown in \eqref{eq:f1}. \begin{equation} \label{eq:f1} \textit{approximated Pi} = \frac{\textit{number of points within the quarter circle}}{\textit{total number of points}} * 4 \end{equation}
The graphical user interface (GUI) is based on a BoarderPane.
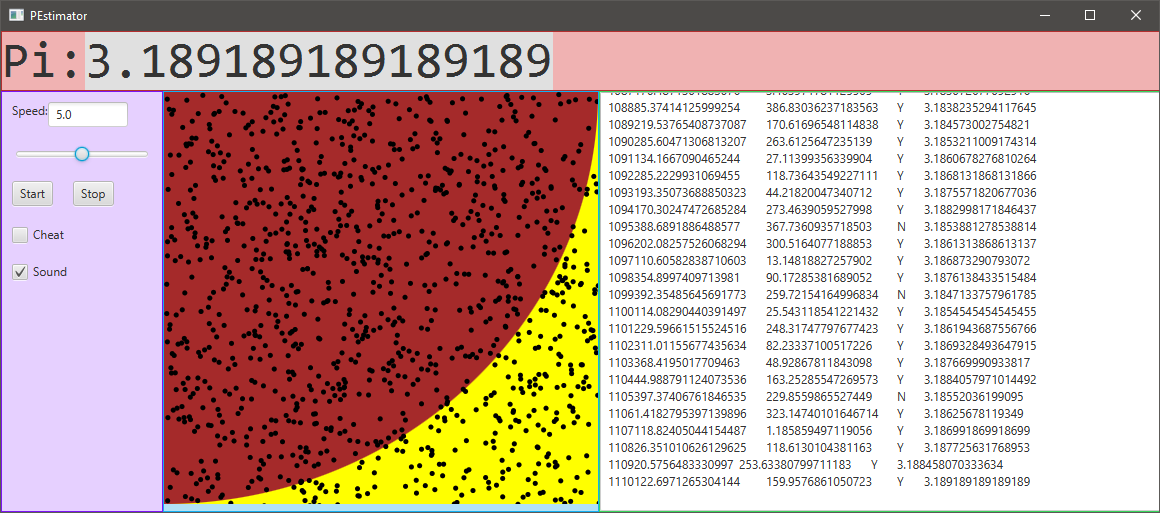
The velocity of adding new points can be regulated on runtime by means of the slider (1‑9). The checkbox «Cheat» will alter the fundamental Pi approximation calculation in the background (see chapter Cheater). The user can also toggle this checkbox by the keystroke combination [CTRL]+[SHIFT]+[C]. The automatically played song can be turned on/off with help of the «Sound» checkbox. The user can toggle this checkbox by the keystroke combination [CTRL]+[SHIFT]+[S] as well. All controls except the slider trigger log entries.
When placing a quarter circle into a square, the radius of the circle is equal the width or the height of the square. Since I choose to enable a variability of the window size, I implemented an oval instead of a circle. Consequently, the user is able to influence the Pi approximation by changing the height-width-ration of the window, respectively of the painting placed in the center section of the BorderPane. The reason for this interference is the following:
As shown in Formula 1, it is crucial to know, how many points are within the quarter circle. These points are considered as «relevant points». While the user is resizing the window, the relevance of the points in the painting may change. Thus, it must be reassessed with help of the quarter circle’s radius which was either the width or the height of the painting when working with a square. Since I implemented an oval instead of a circle, I do not have one simple radius anymore. Therefore, I decided to take the average of the painting’s width and height which then serves as my radius of the quarter oval.
1
2
model.reassessRelevance(
(view.painting.getWidth() + view.painting.getHeight()) / 2);
The class Painting extends the Canvas class. When a painting is constructed, the width and height are being set. Furthermore, the method drawBase is invoked in the constructer which ensures that the painting comes with a yellow background and a red quarter circle, respectively oval.

After the start button was hit, the application begins to add small black points onto the painting randomly. Two of the most important attributes of a Point object are the X and Y coordinate. Firstly, they define where the point will appear on the painting. Secondly, in case the user resizes the application’s window, the coordinates of each existing point get shifted proportionally.
Having the checkbox «Cheat» checked, the Pi obtained by the method getCurrentPi derives from another approximation calculation.
1
2
3
4
5
6
7
8
if (inCheatMode) {
Cheater cheat = Cheater.getlnstance{ );
cheat.approximatePi();
nReturn = cheat.getPi();
}
else {
nReturn = nRelevantPoints / nPoints \* 4;
}
After an object of type Cheater is created, we can approximate Pi in another mathematical way, shown in the public method named approximatePi. It implements the formula \eqref{eq:f2} stated below. Important variable in this approximation is the number of runs \(n\). More runs result in a conciser Pi approximation.
\begin{equation} \label{eq:f2} \textit{approximated Pi (cheated)} = 4 * \sum_{k=1}^n \frac{(-1)^{k+1}}{2k-1} \end{equation}
The Cheater must be initialized by means of the factory method getInstance, since it is a singleton. Additionally, the variables nPi and nRuns are private. Hence, it is possible to call approximate Pi in a very comfortable and easy way, shown in in sample code below.
1
2
3
4
5
Cheater cheat = Cheater.getlnstance();
do {
cheat.approximatePi(); //makes one additional run
cheat.getPi(); //returns current Pi
} while (somelterations);
Consequently, Pi becomes a little bit more precise after each time the method approximtePi was invoked.
Each point added is listed in the text file \PointBook\Point.txt including the approximated Pi up to then. The attributes are tabulator separated, which enables to copy the content and paste it easily in an Excel spreadsheet for some analysis or graph plotting.
The Logger provided in the class ServiceLocator, consists of two handlers. One supports to the console, the other to text files stored in \LogBook. To provide a higher level of structure, I created a custom Formatter called TableFormatter, which basically outputs the information to be logged in a tabulator separated way.
1
2
//creates tab seperated line
String cReturn = cDate + "\t" + cTime + "\t" + cSourceClass + "\t" + cLevel + "\t" + cMessage + "\r\n";
The picture used in the splash screen is a kind of a Pi visualization. Each digit is being represented with one color and then arranged in a nice looking way. More information about the picture can be found here.
Having the sound activated, the user is basically listening Pi. Each digit gets represented with a note and played together with some background music. More information about the song can be found here.
Given that the painting is a perfect square, which leads to the effect that the oval in it can also be considered as a perfect quarter circle. The fact that the points are being added completely randomly influences the approximation of Pi also in a random manner. The graph below shows the evolution of the accuracy of Pi up to 900 points added.
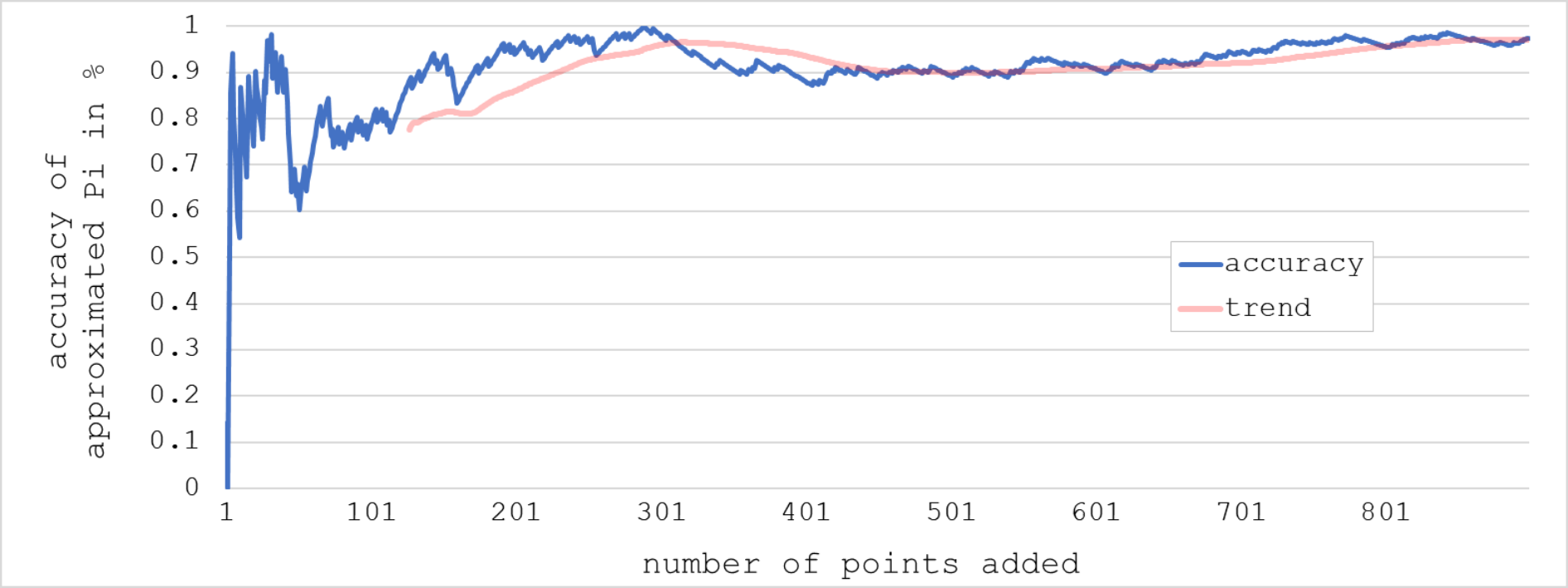
This rather strange development can massively be influenced by the user when resizing the window, as the aspect ration of the painting will alter.
Further insights can be found here:
]]>