How Genetics Helps a Salesman

This article is about solving the famous travelling salesman problem (TSP) with help of a genetic algorithm (GA), implemented with Java.

Before digging into the code, let’s briefly explain this appalling problem.

The Problem

Imagine you defined some locations on a map. Now, you want to travel through all of them within one journey while trying to keep the overall distance at a minimum. Which order would you choose? This may sound like an easy question at first glance. It actually is when talking about three, five or six cities. But what if we talk about 50, 100 or even 10’000 cities? Then you realize how hard this problem is.

You might think, we have computers, so let’s let them do the work. Unfortunately, it’s not that easy because the optimization version of TSP is NP-hard, while its decision version is NP-complete.

Here is why:

As you can see, the number of possible tours increases extremely quickly. The formula assumes a fixed starting city, symmetric distances, and that reversed tours are equivalent. Exhaustively checking every tour soon becomes impractical, although exact TSP algorithms do not simply enumerate all variations.

For TSP, the length of a proposed tour is easy to calculate, but proving that it is the shortest possible tour is harder. In the decision version, however, a proposed tour can be checked efficiently against a given distance bound. You will find a more comprehensive explanation of such NP problems on Wolfram. Additionally, I recommend this video – it may lower the level of weirdness for you (or increase it…).

A Solution

Solving extraordinary problems demands extraordinary approaches. One is a so-called genetic algorithm (GA). Its logic is inspired by natural selection and is often summarized as «the survival of the fittest». Before looking at an implementation of a GA, I kindly invite you to read a bit of theory regarding the algorithm’s structure and behavior.

Components

Element

An element is an exact definition of how to solve the problem. Referring to the TSP, this would be a specific path or route, going through all the cities. This is a possible solution, but it is not necessarily the best one.

Gene

A gene represents the smallest entity in the whole GA. Knowing that an element defines a concrete solution, a gene is one single component of it. Adapted to the TSP, one city or stop within an element is considered to be a gene.

Population

A set of elements forms a population. The number of elements instantiated defines the population’s size. When creating a new population, elements are often constructed at random. Subsequently, the GA tries to evolve its population further in order to develop better elements.

Generation

A current state of a population can be seen as a generation. When evolving the population further, we generate new generations. In other words, a generation is a specific set of elements held in the population.

Fitness

In the evolutionary analogy, fitter individuals are more likely to reproduce. To evaluate which elements are more likely to be selected, we have to assess the quality of each element’s solution in relation to all other solutions. In doing this, we are able to indicate which solutions are better and which are worse, and we can award each of them with an appropriate fitness value. In TSP, the paths with the smallest total distance must be rewarded with the highest fitness. In other problems, this fitness function may differ.

Approach

Selection

Since we try to stimulate our population to evolve a more sophisticated and better version of itself, we should wisely select the elements which may survive a generation. Obviously, we want the genes of those elements with a higher fitness to survive while those with a poor fitness to cease.

Crossover

With just determining the fitness and selecting the fitter elements, we did not optimize our solution to the TSP yet. Therefore, we will apply crossover, like its done in nature during the mating season. This enables to bequeath the qualitative good genomes of two pretty fit elements (depends on the selection) to a new one, which eventually will be part of the population’s next generation.

As an element refers to a specific path in TSP, we extract a random sequence of a fit element’s path (parent 1) and put it into a new element (child). Then, we fill the remaining slots with genes of another fit element (parent 2). This preserves a valid tour and may produce a child fitter than its parents, but it does not guarantee one.

Mutation

Like in the real world, the evolution is influenced by mutation. Crossover only recombines information already present in the parents, whereas mutation introduces additional variation. Hence, it is advisable to include some mutation in a GA.

Once we bred our child element in the TSP, we simply switch the order of the vertices (the genes), representing a concrete path, only very little but randomly.

Evolution

The last and most important part of a GA is the act of repetitively creating new generations (evolving the population). In doing this, we hopefully replace the randomly constructed elements in our initial population with fitter ones over time. However, a population may converge prematurely to an insufficient level of quality. One possible countermeasure is to stop after a certain number of generations, for instance 100, and restart with a new random population.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
 
//take a guess
bestPath = randomPath;

while(!stop) {

    //create a new population
    Population pop = new Population();

    //evolve population a limited number of times
    for (int i=0 ; i < 100 ; i++){

        //create the next generation
        pop.evolve();

        //retrieve the generation's best solution
        Path p = pop.getFittestPath();

        //compare it with the overall best solution
        if(p.distance < bestPath.distance){

            //we've found a better solution
            bestPath = p;
            GUI.repaint(bestPath);
        }
    }

    /* Despite we may have developed an outstanding population,
     * we stop evolving it here and start from scratch again.
     * Possible stopping criteria could be a certain number
     * of newly generated populations or a threshold in
     * the distance improvement of the new best path. */
}
 

Parameters

Since a GA is a heuristic approach to an NP-hard optimization problem, the solution’s quality, as well as the time frame needed to reach a good solution, strongly depends on the custom configuration of some constants (parameters).

For instance, choosing a high population size can increase the possibility of finding a fitter element, but it also raises the computational work. With 5 vertices there are only \(5! = 120\) orderings before accounting for equivalent representations, so a population of 200 may contain many duplicates.

Another important constant is the mutation rate. The level of randomness influencing the GA’s effectiveness is directly linked to it. The more mutation we put in, the fewer genomes will survive a generation identically. A relatively low rate is common, but the effective value depends on the problem representation and other parameters.

To reduce the risk of getting stuck with an unfavorable population, the evolving process can be limited to a maximum number of generations and then restarted. Based on experience with this implementation, a value between 50 and 200 is a useful limit for the number of generations evolved.

Code Extracts

In this chapter, I would like to explain some significant code extracts of my implementation. In order to be more specific, I name from now on a population’s element as a path. Such a path object in my solution only holds integer values in an array, which corresponds to an index in the set of vertices (which is an ArrayList). More precisely, this implementation searches for a shortest Hamiltonian path rather than the closed tour of the conventional TSP. Please be aware, there are numerous other ways to implement these extracts in Java, but here comes mine.

Shuffling

When initiating a population, I would like to randomize the content of all paths in my population.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
 
private void shuffle(int nIntensity) {
    int nMax = this.getLength();
    int nIndexA = -1; //arbitrary
    int nIndexB = -1; //arbitrary
    boolean lExit = false;

    if(nMax == 1) {
        //no need to swap
        lExit = true;
    }

    if(nMax == 2) {
        //swap once
        this.swap(0, 1);
        lExit = true;
    }

    if (! lExit) {
        //swap two elements randomly a certain number of times
        for (int i = 0; i < nIntensity; i++) {
            //set indices equal
            nIndexA = nIndexB;
            //find two different indices
            while (nIndexA == nIndexB) {
                //choose two indices randomly
                nIndexA = (int) (nMax * Math.random());
                nIndexB = (int) (nMax * Math.random());
            }
            //swap those two
            this.swap(nIndexA, nIndexB);
        }
    }
}
 

Ultimately, making two vertices changing its place can simply be achieved by swapping them.

1
2
3
4
5
 
private void swap(int a, int b) {
    int temp = this.Order[a];
    this.Order[a] = this.Order[b];
    this.Order[b] = temp;
}
 

I also make use of the shuffling function when it comes to mutation. In this case, the intensity of mingling is linked to the mutation rate which is a constant provided by the user.

1
2
3
4
5
6
7
8
9
10
11
12
13
 
public void mutate(double nMutationRate) {
    int nIntensity = 0;

    //when mutation rate is 0.4, only 40% of the path be changed
    int len = this.getLength();
    double a = Math.floor(len * Math.abs(nMutationRate));
    nIntensity = (int) a;

    /* Since the mutation is executed by swapping elements,
     * we divide the intensity by two (one swap = two changes). */
    nIntensity = nIntensity / 2;
    this.shuffle(nIntensity);
}
 

Picking

Probably the most important part in the GA is the selection procedure. In order to make the next generation of a population more sophisticated, we have to pick paths wisely before crossing them. One implementation to do the selection could be the following.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
 
//the aim is, to pick a path with a better fitness
//more likely than a path with a smaller fitness
private static Path pickOne(ArrayList<Path> list) {
    Path aReturn = null;
    int index = 0; //assumption
    double r = Math.random();

    /* Imagine we have two elements in the list.
     * The first has a fitness of 0.9 and the second 0.1.
     * We use fitness as the probability of being picked.
     * Math.random() returns a value between 0.0 and 1.0,
     * so the fitter element has a 90% chance of selection. */
    while (r > 0) {
        r = r - list.get(index).getFitness();
        index++;
    }

    //take previous one (the one which caused the loop exit)
    index--;

    //get the path
    aReturn = list.get(index);
    return aReturn;
}
 

This roulette-wheel selection remains valid with a large population as long as the fitness values are normalized and numerical precision is sufficient. I nevertheless implemented another method that directly selects paths by rank.

1
2
3
4
5
6
7
8
9
10
11
 
private static Path pickRank(ArrayList<Path> list, int nIndex) {
    Path aReturn = null;
    ArrayList<Path> clonedList = new ArrayList<Path>(list);

    //sort paths by descending fitness
    clonedList.sort((p1, p2) -> Double.compare(p2.getFitness(), p1.getFitness()));

    //get the required path
    aReturn = clonedList.get(nIndex);
    return aReturn;
}
 

After the provided list of paths is sorted by fitness in descending order, this static function can pick a path by rank. In first place is the fittest path, in second place the second-fittest path and so on. This makes it possible to pick the two fittest paths and create all child paths from them, although doing so reduces genetic diversity.

Crossing

Once two paths have been picked, I cross them over. The number of genes originating from the first path, respectively from the second path, is defined randomly. Alternatively, one could also set the shares to 50%.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
 
private static Path cross(Path p1, Path p2) {
    Path aReturn = null;
    int nLength = p1.getLength();
    int nSequenceLength = (int) (nLength * Math.random());

    //set minimum length
    if (nSequenceLength == 0) {
        nSequenceLength = 2;
    }

    //decrease length
    if (nSequenceLength == nLength) {
        nSequenceLength -= 2;
    }

    //define start index randomly
    int nStartIndex = (int) ((nLength - nSequenceLength) * Math.random());

    //initiate a new order (child path)
    int[] order = new int[nLength];

    //put -1 into each slot as a placeholder
    for (int i = 0; i < nLength; i++) {
        order[i] = -1;
    }

    //fill in genome of first parent path
    for (int i = nStartIndex; nSequenceLength > 0; i++) {
        order[i] = p1.get(i);
        nSequenceLength--;
    }

    //fill in genome of second parent path
    int n=0;
    for (int i = 0; i < nLength; i++) {
        if (order[i] == -1) {
            //fillable slot found
            boolean lExit=false;
            while(!lExit) {
                //check if vertex-index already included
                if (Path.contains(order, p2.get(n))) {
                    n++;
                } else {
                    lExit = true;
                }
            }
            order[i] = p2.get(n);
        }
    }
    aReturn = new Path(order);
    return aReturn;
}
 

Since both the start index and the sequence length are arbitrarily defined, my child path could be composited in various ways. The picture below visualizes one of them.

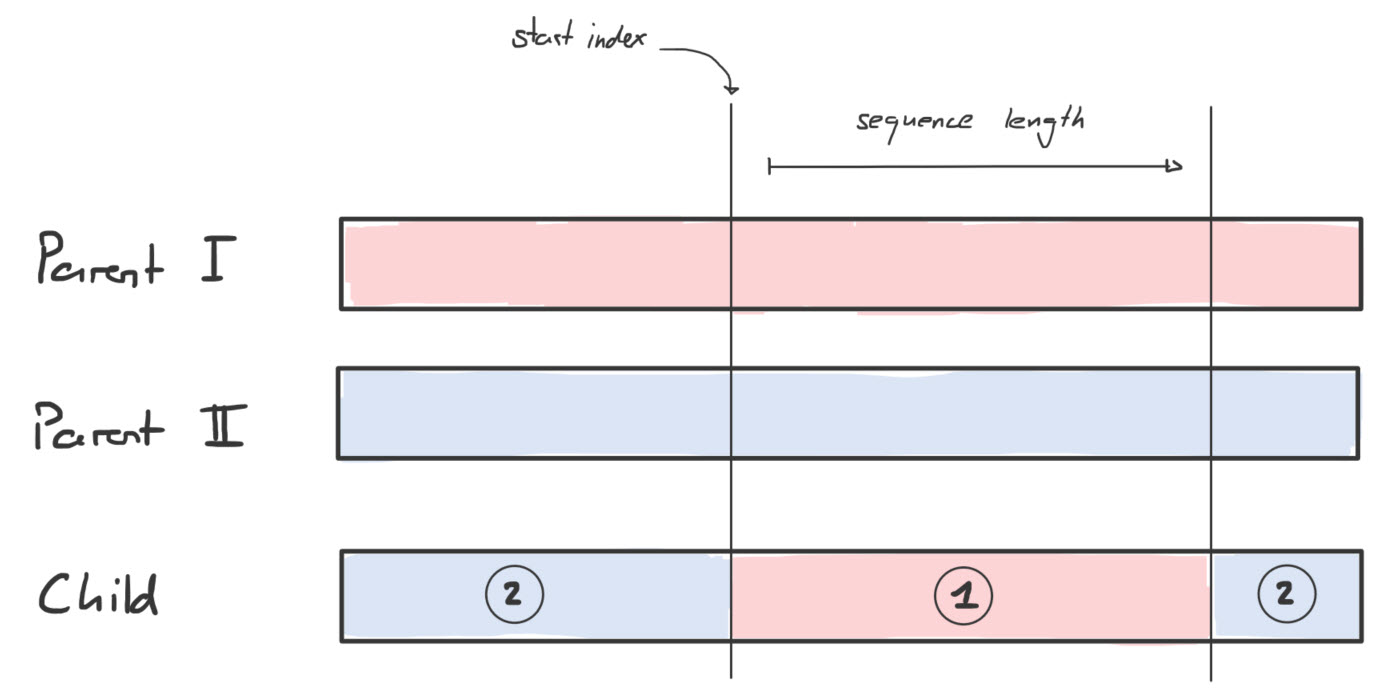
Evolving

After exploring the components of a GA, the cooperation of them, using the PickOne method, would look like this.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
 
public void evolve() {
    ArrayList<Path> ps_new = new ArrayList<Path>();
    this.assessFitness();

    for (int i = 0; i < this.ps.size(); i++) {
        Path p1 = pickOne(this.ps);
        Path p2 = pickOne(this.ps);
        Path p3 = cross(p1, p2);
        p3.mutate(this.nMutationRate);
        ps_new.add(p3);
    }

    this.ps = ps_new;
}
 

To make usage of the more target-aimed method PickRank, I created the following alternative.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
 
public void evolve2() {
    ArrayList<Path> ps_new = new ArrayList<Path>();
    this.assessFitness();
    Path p1 = pickRank(this.ps, 0);
    Path p2 = pickRank(this.ps, 1);

    while(ps_new.size() < this.ps.size()) {
        Path p3 = cross(p1, p2);
        p3.mutate(this.nMutationRate);
        ps_new.add(p3);
    }

    this.ps = ps_new;
}
 

Conclusion

The genetic algorithm approach is just one way to tame the travelling salesman problem. From my point of view, its parallels to the evolutionary process in the real world make it comprehensible and fun to implement. For sure, there are other interesting problem-solving approaches like the so-called simulated annealing or ant colony optimization algorithms.

In case you would like to dig deeper in this fascinating TSP, I recommend exploring this page. It provides historical information, other solving concepts, solution quality assessments and more.

• Source Code