The PEstimator is an Java application which approximates the irrational mathematical constant Pi. The base for the approximation is a quarter circle within a rectangle. On this painting, points will be added iteratively. The ration of the number of points within the quarter circle to the total number of points, multiplied by four equals Pi over time, as shown in \eqref{eq:f1}.

\begin{equation} \label{eq:f1} \textit{approximated Pi} = \frac{\textit{number of points within the quarter circle}}{\textit{total number of points}} * 4 \end{equation}

The Interface

The graphical user interface (GUI) is based on a BoarderPane.

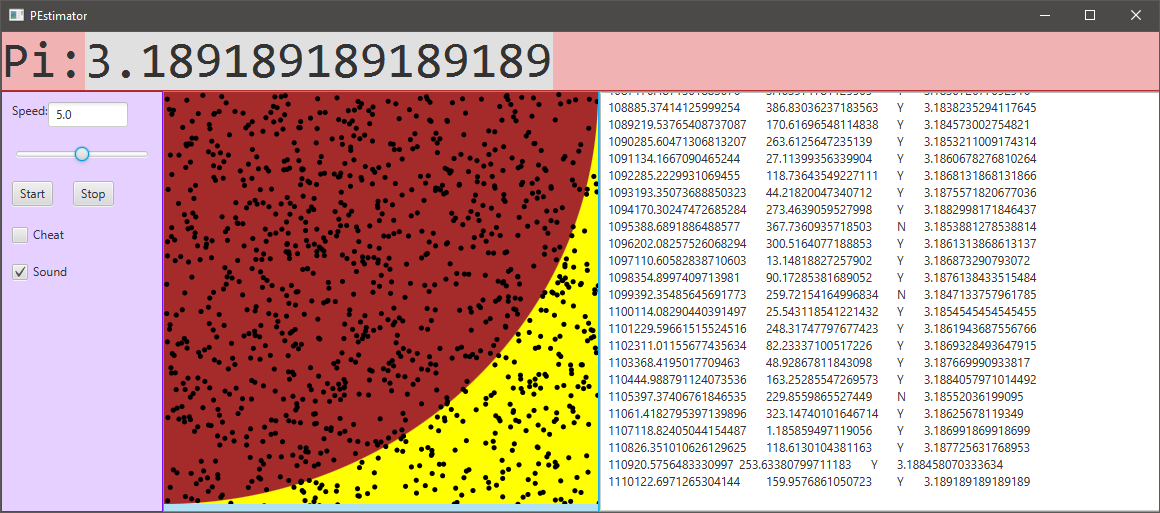
Control Elements

The velocity of adding new points can be regulated on runtime by means of the slider (1‑9). The checkbox «Cheat» will alter the fundamental Pi approximation calculation in the background (see chapter Cheater). The user can also toggle this checkbox by the keystroke combination [CTRL]+[SHIFT]+[C]. The automatically played song can be turned on/off with help of the «Sound» checkbox. The user can toggle this checkbox by the keystroke combination [CTRL]+[SHIFT]+[S] as well. All controls except the slider trigger log entries.

Resizing the Window

When placing a quarter circle into a square, the radius of the circle is equal the width or the height of the square. Since I choose to enable a variability of the window size, I implemented an oval instead of a circle. Consequently, the user is able to influence the Pi approximation by changing the height-width-ration of the window, respectively of the painting placed in the center section of the BorderPane. The reason for this interference is the following:

As shown in Formula 1, it is crucial to know, how many points are within the quarter circle. These points are considered as «relevant points». While the user is resizing the window, the relevance of the points in the painting may change. Thus, it must be reassessed with help of the quarter circle’s radius which was either the width or the height of the painting when working with a square. Since I implemented an oval instead of a circle, I do not have one simple radius anymore. Therefore, I decided to take the average of the painting’s width and height which then serves as my radius of the quarter oval.

1
2
 
model.reassessRelevance(
(view.painting.getWidth() + view.painting.getHeight()) / 2);
 

Painting

The class Painting extends the Canvas class. When a painting is constructed, the width and height are being set. Furthermore, the method drawBase is invoked in the constructer which ensures that the painting comes with a yellow background and a red quarter circle, respectively oval.

Point

After the start button was hit, the application begins to add small black points onto the painting randomly. Two of the most important attributes of a Point object are the X and Y coordinate. Firstly, they define where the point will appear on the painting. Secondly, in case the user resizes the application’s window, the coordinates of each existing point get shifted proportionally.

Cheater

Having the checkbox «Cheat» checked, the Pi obtained by the method getCurrentPi derives from another approximation calculation.

1
2
3
4
5
6
7
8
 
if (inCheatMode) {
Cheater cheat = Cheater.getlnstance{ );
cheat.approximatePi();
nReturn = cheat.getPi();
}
else {
nReturn = nRelevantPoints / nPoints \* 4;
}
 

After an object of type Cheater is created, we can approximate Pi in another mathematical way, shown in the public method named approximatePi. It implements the formula \eqref{eq:f2} stated below. Important variable in this approximation is the number of runs \(n\). More runs result in a conciser Pi approximation.

\begin{equation} \label{eq:f2} \textit{approximated Pi (cheated)} = 4 * \sum_{k=1}^n \frac{(-1)^{k+1}}{2k-1} \end{equation}

The Cheater must be initialized by means of the factory method getInstance, since it is a singleton. Additionally, the variables nPi and nRuns are private. Hence, it is possible to call approximate Pi in a very comfortable and easy way, shown in in sample code below.

1
2
3
4
5
 
Cheater cheat = Cheater.getlnstance();
do {
cheat.approximatePi(); //makes one additional run
cheat.getPi(); //returns current Pi
} while (somelterations);
 

Consequently, Pi becomes a little bit more precise after each time the method approximtePi was invoked.

Behind the Scenes

PointBook

Each point added is listed in the text file \PointBook\Point.txt including the approximated Pi up to then. The attributes are tabulator separated, which enables to copy the content and paste it easily in an Excel spreadsheet for some analysis or graph plotting.

LogBook

The Logger provided in the class ServiceLocator, consists of two handlers. One supports to the console, the other to text files stored in \LogBook. To provide a higher level of structure, I created a custom Formatter called TableFormatter, which basically outputs the information to be logged in a tabulator separated way.

1
2
 
//creates tab seperated line
String cReturn = cDate + "\t" + cTime + "\t" + cSourceClass + "\t" + cLevel + "\t" + cMessage + "\r\n";
 

Splash-Screen

The picture used in the splash screen is a kind of a Pi visualization. Each digit is being represented with one color and then arranged in a nice looking way. More information about the picture can be found here.

Sound

Having the sound activated, the user is basically listening Pi. Each digit gets represented with a note and played together with some background music. More information about the song can be found here.

Evolution of approximated Pi

Given that the painting is a perfect square, which leads to the effect that the oval in it can also be considered as a perfect quarter circle. The fact that the points are being added completely randomly influences the approximation of Pi also in a random manner. The graph below shows the evolution of the accuracy of Pi up to 900 points added.

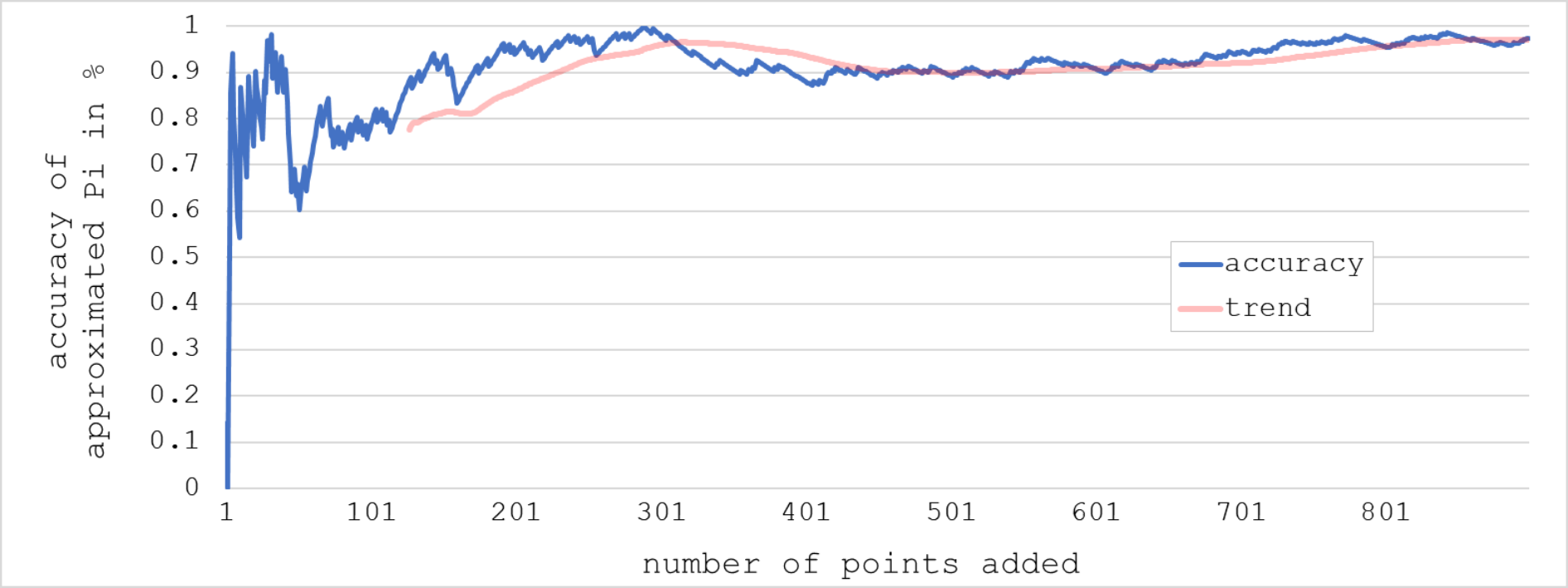
This rather strange development can massively be influenced by the user when resizing the window, as the aspect ration of the painting will alter.

Further Resources

Further insights can be found here:

• Source code